Are Vehicle Damage and Occupant Injury Always Proportional?

Abstract

Minor vehicle damage in the presence of serious occupant injury is a frequent occurrence in acceleration-deceleration (rear-end) automobile collisions. Damage to the struck automobile and the degree and severity of injury to its occupants is explored. Special consideration is given to the physical factors that have been shown to increase the application of force of the collision to the vehicle's occupants. A brief physics glossary follows the article.

Introduction

In the day to day practice of treating patients injured in acceleration-deceleration automobile collisions, the question is often asked, "Why is it that a great deal of injury can be sustained by the driver or passengers of the struck vehicle, when only a relatively small amount of damage was done to the vehicle itself?" This question makes reference to a common misconception about the acceleration-deceleration automobile collision -- namely, that vehicle damage and occupant injury are proportional. To truly understand this complex relationship, a review of the mechanics of the collision is necessary, since the physical forces involved in the collision must be understood to provide insight as to how injury can exist in the absence of a large amount of damage to the struck vehicle itself.

Mechanics of the Collision

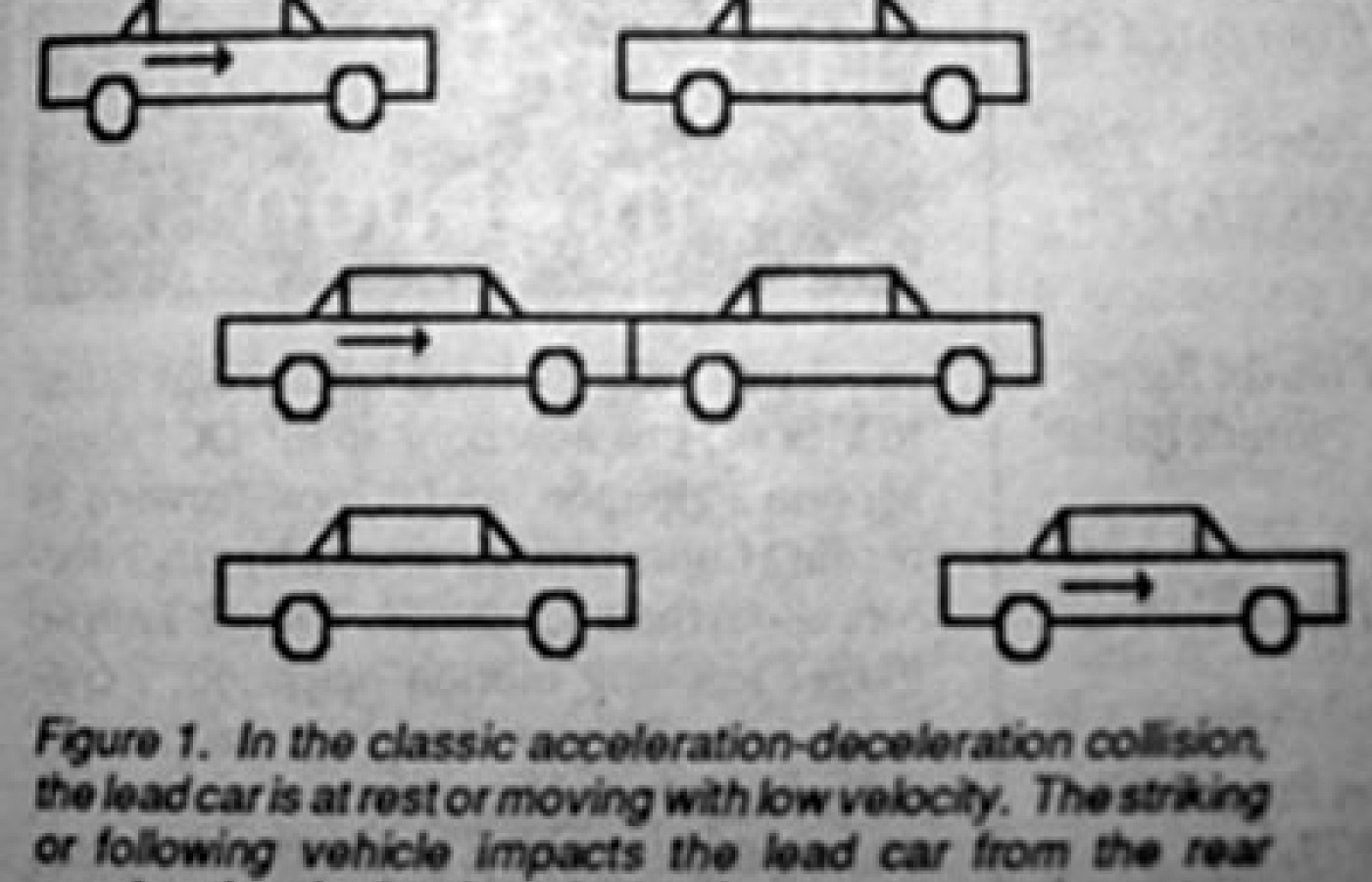
An acceleration-deceleration collision classically involves two vehicles, the lead vehicle or struck vehicle and the striking or following vehicle. The lead vehicle is usually slowed or stopped at an intersection and is impacted forcibly from the rear by the striking vehicle (See Figure 1). The force of the impact then causes the lead vehicle to be propelled forward some distance until it comes to rest. The amount of force applied to the rear of the lead vehicle is, of course, dependent upon a number of variables, specifically, the weight and velocity of the striking vehicle.

The amount of acceleration attained by the lead vehicle, as a result of the collision, is dependent upon the force applied by the striking vehicle, the weight or amount of inertia of the lead vehicle, and lastly upon factors that will allow the lead vehicle to roll easily. For example, slick road conditions, whether the brakes were applied at the time of the collision, automatic or manual transmission, and whether the lead vehicle was completely stationary or slightly moving. (1) As we shall see, a vehicle that is more easily accelerated will generally sustain a lesser amount of damage than one that does not accelerate, given the same intensity of force application.

Acceleration of the Lead Vehicle

As mentioned above, the ease with which the lead vehicle is accelerated may have a direct bearing on the amount of sustained damage. This has to do with the fact that if the energy of the striking vehicle is expended in an effort to accelerate the lead vehicle forward, less energy is absorbed by the lead vehicle in a manner that will cause damage to its structure. The reverse situation would also be true of the lead vehicle that is not accelerated -- if it is not accelerated, the energy expended by the striking vehicle in the collision is absorbed by the lead vehicle in the form of twisted metal, broken glass, etc.

The prevailing road conditions (icy or wet versus dry), the composition of the road (loose gravel versus pavement), whether the driver of the lead vehicle had his foot applied to the brakes, and the weight or inertia of the lead vehicle are all factors that will affect how easily acceleration will be achieved. For example, it should be obvious that a mid-size vehicle on icy roads, with the driver's foot off the brake will accelerate much more easily when struck from behind than, say, a full-size automobile on dry pavement, with the brakes engaged.

Magnitude of the Acceleration of the Lead Vehicle

Several medical investigators have studied acceleration-deceleration collisions in detail.^1,2,3,4,5 The time period for contact between the lead and striking vehicles varies in the literature from 0.1 second to 0.2 seconds. Figure 2 illustrates the measured acceleration of the lead vehicle during this short period of time. Most investigators use multiples of the force of gravity (g) to relate the horizontal acceleration of the car to our everyday experience of weight. For example, a force that is twice the force of gravity (2g) would double the effective weight of an object, that is to say, 150 lb. man, under a 2g force would weigh 300 lbs.

Severy⁵ has shown that an eight mile per hour rear-end collision will produce an acceleration of the lead vehicle of two times the force of gravity (2g), with an impact duration of 0.2 seconds. Panjabi and White⁶ state that a 10.8 mile per hour rear-end collision with an impact duration of 0.1 second will produce an acceleration of the lead vehicle that has a magnitude of five times the force of gravity (5g). The significance that this information has to our discussion is that collisions occurring at relatively low velocities can result in large forces being applied to the lead vehicle.

To review, the more easily the lead car is accelerated, the less likely it is to sustain damage, and under the proper conditions, relatively low velocities can result in a great deal of force being applied to the lead vehicle. Or, in more practical terms, easy acceleration of the lead vehicle, almost regardless of the magnitude of the forces involved, is the friend of the property damage insurance adjustor. Unfortunately, as we shall soon see, easy acceleration of the lead vehicle is the enemy of the occupants of the struck vehicle.

Next issue: Part Two, the conclusion of, "Are Vehicle Damage and Occupant Injury Always Proportional?"

Glossary of Physics Terms

A. Linear/translatory motion: The progression of all parts of a body in the same direction, the same distance, and at the same rate of speed. Example: a car traveling down a road.

B. Angular/rotatory motion: Movement in an arc about a fixed point.

C. Center of mass/gravity: The point of a body which acts as though the entire the entire mass of body is concentrated at that single point (balancing point).

D. Velocity: The rate of change of position with respect to time. Mathematically: Distance1 - Distance2/Time.

E. Acceleration: The rate of change of velocity with respect to time. Mathematically: Velocity1 - Velocity 2/time. Acceleration is independent of the magnitudes of the involved velocities.

F. Inertia: The tendency of an object at rest to remain at rest or of an object in motion to remain in motion; i.e., the resistance of an object to change. A simple measure of inertia is weight, the greater the weight of an object, the greater the inertia it possesses.

G. Mass: A property of matter that is a direct measure of inertia; i.e., as above the greater the mass of an object, the greater the inertia or resistance to change.

H. Weight: The interaction of matter with the accelerating force of gravity. Mathematically: weight = mass x gravity.

I. Momentum: A property possessed by an object in motion. Mathematically: Momentum = mass x velocity.

J. Friction: The force that resists motion between two surfaces in contact. Friction is dependent upon the mass of the objects in contact and their frictional coefficients. Static (stationary) frictional forces are greater than kinetic (moving) frictional forces; i.e., it is easier to keep an object moving than it is to start that object moving. Anything that increases frictional forces essentially increases the functional inertia of the objects in contact.

References

1. McNab, I. "Acceleration Extension Injuries of the Cervical Spine." The Spine, vol. II. Rothman, Richard, and Simeone 1975.
2. McNab, I. "Acceleration Injuries of the Cervical Spine." J. Bone Joint Surg. 1964; 46A:1797.
3. Martinez, J.; Garcia, D. "A Model for Whiplash." J. Biomech. 1968; 1:23.
4. McKenzie, J.; Williams, J. "The Dynamic Behavior of the Head and Cervical Spine During 'whiplash'." J. Biomech. 1971; 4:477.
5. Severy, D.; Mathewson, J.; Bechtol, C. "Controlled Automobile Related Engineering and Medical Phenomena." "Medical Aspects of Traffic Accidents. Proceedings of Montreal Conference, p. 52, 1955.
6. White, A.; Panjabi, M. Clinical Biomechanics of the Spine. Philadelphia: Lippincott 1978.
7. Bailey R. The Cervical Spine. Philadelphia: Lippincott 1983.
8. Cailliet R. Neck and Arm Pain. Philadelphia: F.A. Davis Co. 1977.
9. Turek S. Orthopaedics: Principles and Their Application. Philadelphia: Lippincott 1977.
10. Ommaya, A.; Hirsch, A. "Tolerances for Cerebral Concussion from Head Impact and Whiplash in Primates." J. Biomech. 1971; 4:13.